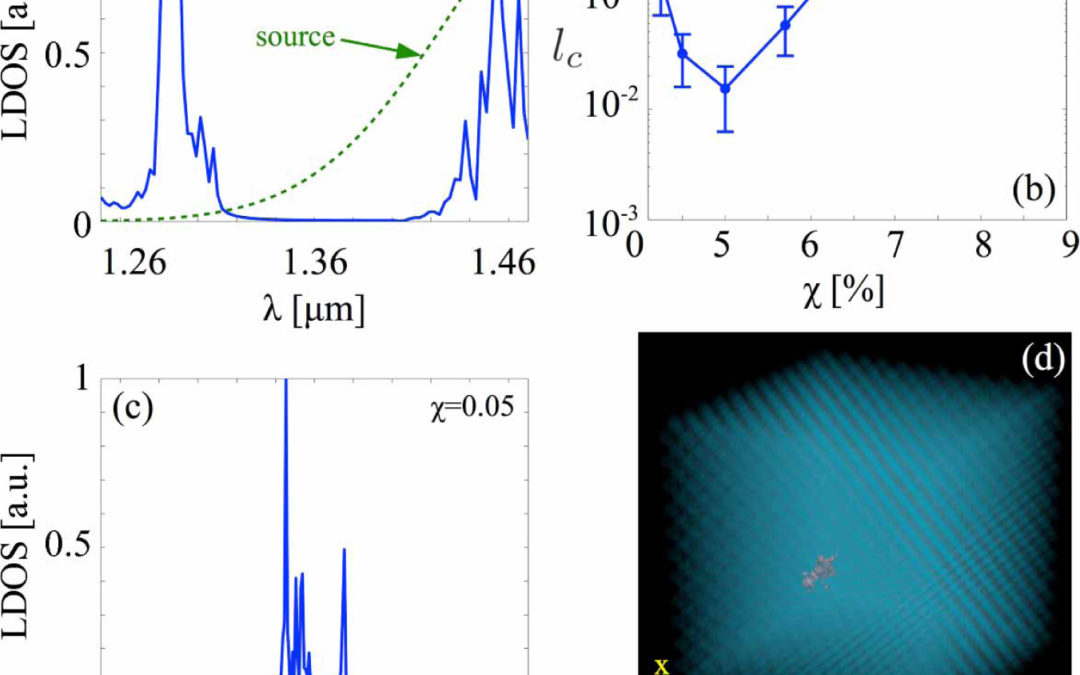
By employing Random Matrix Theory (RMT) and first-principle calculations, we investigated the behavior of Anderson localization in 1D, 2D and 3D systems characterized by a varying disorder. In particular, we considered random binary layer sequences in 1D and structurally disordered photonic crystals in two and three dimensions. We demonstrated the existence of a unique optimal degree of disorder that yields the strongest localization possible. In this regime, localized modes are constituted by defect states, which can show subwavelength confinement properties. These results suggest that disorder offers a new avenue for subwavelength light localization in purely dielectric media.

Recent Comments