ECE231 Introduction to Optics

Please click here to download an updated sillaby with detailed information on the course.
Class Notes
| Last Update | Topic | Summary | Slides |
| 4-Sep-2019 | Revision of elementary EM | Maxwell’s equations in isotropic media. Poynting theorem. Definition and physical meaning of the Poynting vector and the energy density of the electromagnetic wave. Complex formalism. Time average of products of sinusoidal functions. Definition of optical intensity. Plane-wave solutions of Maxwell’s equations. | lesson 1 |
| 18-Aug-2019 | Geometrical Optics | Introduction to geometrical optics and the concept of rays. Optical path. Fermat Principle of least time: variations formulation. Fermat principle from Maxwell Equations: limits of geometrical optics. The propagation of rays. Examples of Ray Tracing. | lesson 2 |
| 18-Oct-2020 | Geometrical Optics | Introduction to Matrix optics. ABCD matrix. Refraction matrix, propagation matrix, and reflection matrix. Significance of matrix elements. Lenses. Thick and thin lenses. Imaging formation by thin lenses. The human eye. A brief discussion of chromatic and spherical aberrations of lenses. Elements of microscope theory: infinity-corrected systems. Microscope resolution. Microscope objectives. Gallery of microscopes techniques. | lesson 3 |
| 18-Aug-2021 | Diffraction theory | The scalar theory of diffraction. Sommerfield’s definition of diffraction. Discussion and theoretical justification of the scalar approximation. Helmholtz equation for the disturbance field. Intensity observable in the scalar approximation. The classical approach to the diffraction problem: definition of propagation and interaction problems. | lesson 4 |
| 13-Oct-2023 | Diffraction theory | The first example of a propagation problem: interference of two noncollinear plane waves. Analysis of intensity distribution. Definition of interference fringes and discussion on possible applications. Spherical waves. | lesson 5 |
| 13-Oct-2023 | Diffraction theory | A brief introduction to coherence and interference effects in coherent fields. Discussion of applications of Newton’s rings. Interference between spherical waves and plane waves. | lesson 6 |
| 18-Aug-2019 | Diffraction theory | Bessel beam solution of the Helmholtz equations. Field distribution and dispersionless propagation. Discussion and experimental generation of Bessel beams. | lesson 7 |
| 18-Aug-2019 | Diffraction theory | Experimental generation of Bessel beam; discussion on possible applications of Bessel beams; Elements of linear system theory and Fourier analysis. Exercises set before the midterm evaluation. | lesson 8 |
| 18-Aug-2019 | Diffraction theory | The propagation problem. General solution through Fourier modal decomposition. Plane-wave propagator. Linear system representation. Evanescent waves and their physical implications. | lesson 9 |
| 19-Nov-2020 | Diffraction theory | The first formula of Rayleigh-Sommerfield. Huygens principle. Fresnel diffraction integral. Far-Field diffraction formula. Optical resolution limits from wave propagation. Exercise set on far-field diffraction from the slit and simple optical apertures. | lesson 10 |
| 18-Aug-2019 | Diffraction theory | Modeling of laser light beams. General considerations on laser light properties. Derivation of Paraxial wave equation. | lesson 11 |
| 18-Aug-2019 | Diffraction theory | Spherical waves and Gaussian beam solutions of the paraxial wave equation. Curvature, waist, and general properties of Gaussian beams. | lesson 12 |
| 18-Aug-2019 | Diffraction theory | Direct and Inverse problem of Gaussian beams. The physical explanation of the diffraction of a Gaussian beam in terms of the dispersion relation. ABCD Law of Gaussian beams. Free space propagation ABCD matrix. The interaction problem: a general approach through the transfer function. Exact solution of the interaction with a semi-infinite metallic plane; comparison with the transfer function method; discussion. | lesson 13 |
| 18-Aug-2019 | Diffraction theory | The thin lens. The transfer function of the thin lens. Application of the thin lens to visualize the far field part II) The action of a thin lens on a Gaussian Beam. Collimation and Focusing problem. Beam Expander. ABCD matrix of a thin lens. | lesson_14 |
| 18-Aug-2019 | Diffraction theory | Gratings. General properties and different examples of applications | lesson 15 |
| 18-Aug-2019 | Waveguide theory | Analysis of dispersion relation of the symmetric waveguide. TE and TM modes. Number of modes for a given geometry. Asymmetric waveguides: study of the general case. Modal profile of guided modes. | lesson 16 |
| 18-Aug-2019 | Waveguide theory | The Fabry-Perot interferometer. Reflection and Transmission from multiple rays. Airy’s Formulae. Finesse. Interferometer resolving power. | lesson 17 |
| 18-Aug-2019 | Optical resonators | Optical cavities. ABCD transfer matrix approach. Stability analysis. Gaussian mode solution of cavities made by spherical mirrors. Phase and amplitude self-consistent equations. | lesson 18 |
Final 2023 results
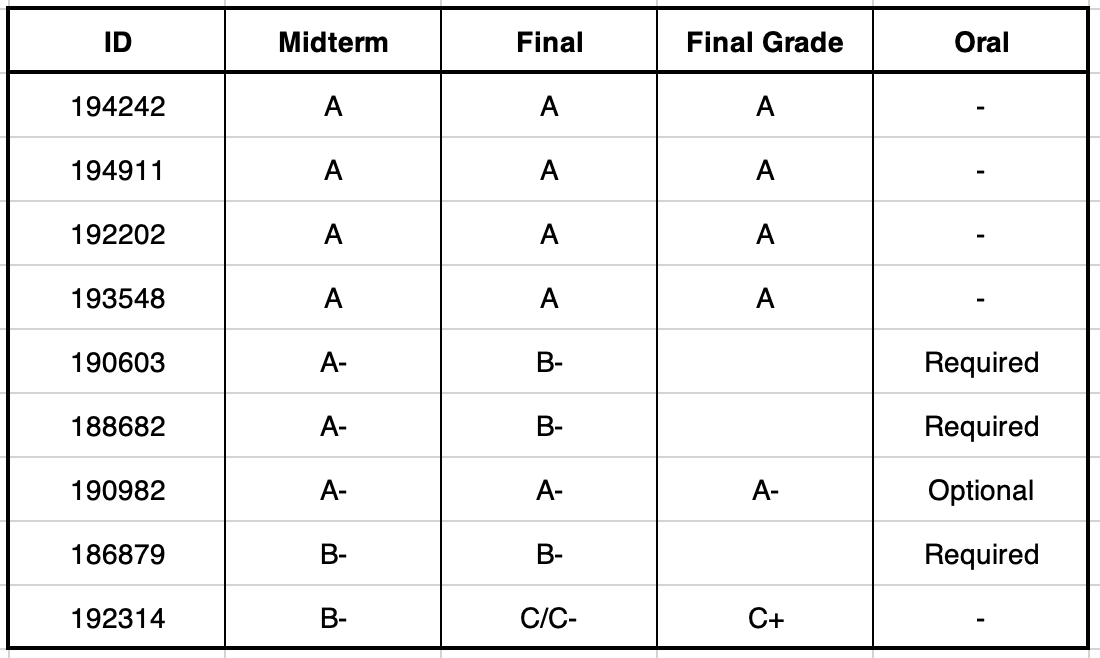
For the students with a passing average grade who are required to do the oral, I will meet them in my office building 1, level 4, room 4305, on Sunday 10 at the following times:
190603: 10am
188682: 10:30am
186879: 11am
